关系运算
关系代数运算符主要有4类:
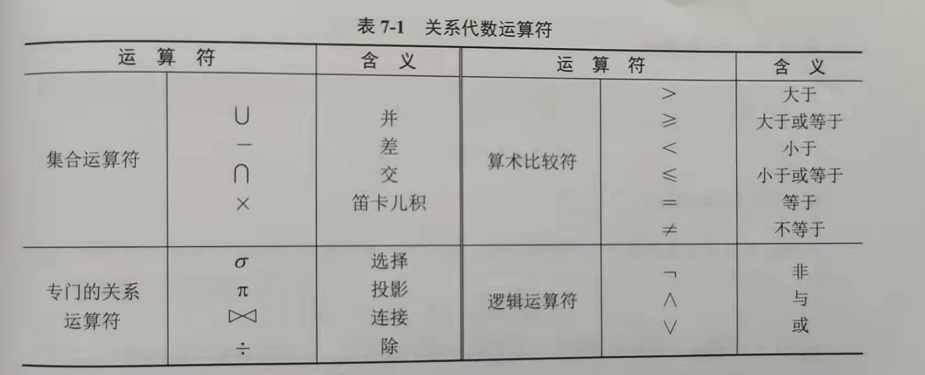
Relational Algebra / 关系代数符号可以用于表达数据库标准操作逻辑。
常用符合及对应的 LATEX如下
| Operation | 中文 | 符号 | LATEX |
|---|---|---|---|
| Projection | 投影 | Π | \Pi |
| Selection | 选择 | σ | \sigma |
| Renaming | 重命名 | ρ | \rho |
| Aggregate Function | 聚合函数 | G | \mathcal{G} |
| Union | 交 | ∩ | \cap |
| Intersection | 补 | ∪ | \cup |
| Natural Join | 自然连接 | ⋈ | \bowtie |
| Left Outer Join | 左外连接 | ⟕ | … 这几个直接复制吧 |
| Right Outer Join | 右外连接 | ⟖ | |
| Full Outer Join | 全外连接 | ⟗ | |
| Cartesian product | 笛卡尔乘积 | × | \times |
| Divide | 除 | ÷ | \div |
| Assignment | 赋值 | ← | \leftarrow |
| And | 条件并列 | ∧ | \land or \vee |
| Negation | 非 | ¬ | \neg |
| Exist | 存在 | ∃ | \exists |
| For All | 对所有 | ∀ | \forall |
| 下标文字 | σusername | _{\text{}} | |
| 粗体文字 | Gcount(*) | \textbf{} | |
| 长长长长括号 | (((( | \big( \Big( \bigg( \Bigg( | |
| 比较 | >≥<≤≠ | \gt \ge \lt \le \ne |
五种基本的关系代数运算
五种基本的关系代数运算包括并、差、笛卡尔、选择和投影。
1️⃣ 并Union
如果关系R和关系S具有相同的关系模式,即R与S的元组数相同(结构相同)。
则关系R与关系S的并集由属于R或属于S的元组构成的集合组成, 记作 R∪S
2️⃣ 差 Difference
关系R与关系S的差集由属于R但不属于S的元组构成的集合组成, 记作 R-S
3️⃣ 广义笛卡尔积 Extended Cartesian Product
两个元数分别为n目和m目的关系R和S 的广义笛卡尔积是一个(n+m)列的元组的集合。记作 R × S
如果R和S中有相同的属性名,可在属性名前加关系名作限定,以示区别。
若,R有K1个元组,S有K2个元组,则R和S的广义笛卡尔积有K1 ×K2个元组(也称基数为K1 ×K2)。
4️⃣ 投影 Projection
投影运算是从关系的垂直方向进行运行。
即在关系R中选择若干属性列A组成新的关系,记作 πa (R)
5️⃣ 选择 Selection
选择运算是从关系的水平方向进行运算。
即从关系R中选择满足给定条件的元组,记作 σF(R)
⭐ 注意:
F中的运算对象是属性名(或列的序号)或常数,可以是比较运算符或逻辑运算符。
列的序号使用数字表示,常数需要添加单引号。
例如:
σ1>6(R) :表示选取R关系中第一个(列)属性值大于第六个(列)属性值的元组。
σ1>'6'(R) : 表示选取R关系中第一个(列)属性值大于6的元组。
扩展的关系运算
扩展的关系运算可以从基本的关系运算中导出,主要包括: 交、连接、除、广义投影、外连接、聚集函数等。
1️⃣ 交集 Intersection
关系R与关系S具有相同的关系模式,两者的交集,是由属于R同时又属于S的元组组成的集合,记作 R∩S
R ∩ S = R - (R - S) 或 R ∩ S = S - (S - R)
2️⃣ 连接Join
连接分为 θ 连接、等值连接、以及自然连接三种。
注意:
连接运算总是从连个关系R和S的笛卡尔积中选取满足条件的元组。
因此,可以认为笛卡尔积是无条件连接,其他是有条件连接。
- θ 连接
即从笛卡尔积中选取属性间满足一定条件的元组。
θ 为连接的条件,是比较运算符。
⭐ P262页例题
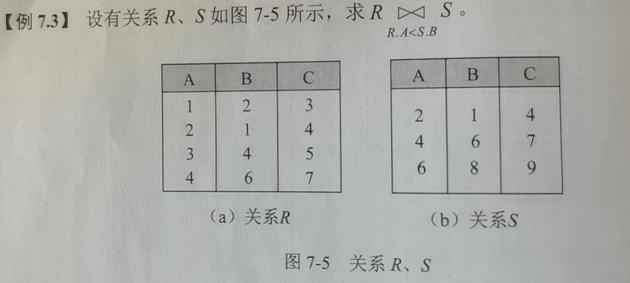
结果集合为RXS后选取满足条件(r.a< s.b)的元组。
对应sql为:
select r.A as RA ,r.B as RB ,r.C as RC,s.A as SA ,s.B as SB ,s.C as SC from r,s where r.a< s.b
-- 结果
RA|RB|RC|SA|SB|SC|
--+--+--+--+--+--+
1| 2| 3| 6| 8| 9|
1| 2| 3| 4| 6| 7|
2| 1| 4| 6| 8| 9|
2| 1| 4| 4| 6| 7|
3| 4| 5| 6| 8| 9|
3| 4| 5| 4| 6| 7|
4| 6| 7| 6| 8| 9|
4| 6| 7| 4| 6| 7|- 等值连接 Equijoin
当θ 为 “=” 时,如 r.a = s.b 称之为 等值连接
等值联结也称为内部联结。
对应于sql语句而言,等值连接还可以使用 inner join on 语法。 如:
SELECT prod_name,prod_price,vend_name
FROM vendors
INNER JOIN products
ON vendors.vend_id = products.vend_id
ORDER BY vend_name- 自然连接 Natural join
自然连接是一种特殊的等值连接,它要求两个关系中进行比较的分量必须是相同的属性值,并且在结果集中将重复的属性列去掉。
因此,自然连接可以由基本的关系运算笛卡尔积和选取运算导出。
即自然连接,同时从关系的水平方向和垂直方向运算,如果没有重复属性,那么自然连接就转化为笛卡尔积。
⚡ 自然连接记作: R ⋈ S
Tip
即:自然联结和内部联结的区别是,自然联结不会出现相同的重复列。
⭐ 另外,注意:除了自然连接,还有自连接。
如果FROM自己联结的两个表(标记了别名)是同一个表,则称为自联结。
自连接(self join)是连接的一种用法,但并不是连接的一种类型,因为他的本质是把一张表当成两张表来使用。
-- 注意,在显示列时,务必都加上表别名的前缀
-- 虽然自联结联结的是同一个表,但是mysql并不关心这个
select
p1.prod_id,
p1.prod_name,
p1.vend_id
from
products as p1,
products as p2
where
p1.vend_id = p2.vend_id
and p2.prod_id = 'DTNTR'
-- output
prod_id|prod_name |vend_id|
-------+--------------+-------+
DTNTR |Detonator | 1003|
FB |Bird seed | 1003|
FC |Carrots | 1003|
SAFE |Safe | 1003|
SLING |Sling | 1003|
TNT1 |TNT (1 stick) | 1003|
TNT2 |TNT (5 sticks)| 1003|3️⃣ 除 Division
除运算是同时从关系的水平方向和垂直方向进行运算。
⭐ P263 例7.5
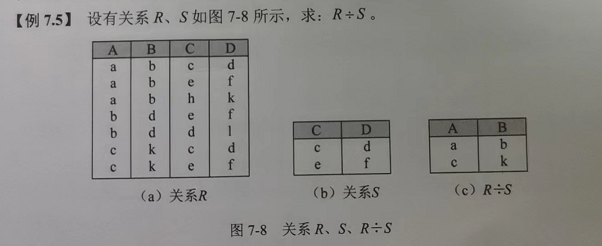
解题步骤:
- 找出R、S共同的列 CD。
- 找出R中可能的组合取值 a, b, b, d,c, k
- a, b 有 c, d, e, f,h, k 种组合(象集);
- b, d 有 e, f,d, l 种组合(象集);
- c, k 有 c, d, e, f 种组合(象集);
- 可知 a, b 和 c, k 中的组合全覆盖 关系S。
- 所以,结果为: a, b 和 c, k ,如上图。
提示:
关系R 和 关系S 拥有共同的属性 CD, R ÷ S 得到的属性就是关系R包含,而关系S不包含的属性,即AB属性。
4️⃣ 广义投影 generalized projection
广义投影允许在投影列表中使用算术运算符,实现了对投影运算的扩充。
对应sql举例
-- 水果关系表fruit如下,水果名称,单价,数量
name price quantity
apple 8 100
banana 6 80
-- 求每种水果的价值
name worthy
apple 8*100
banana 6*80
-- sql 如下
select name, price*quantity as worthy from fruit5️⃣ 外连接 outer join
外连接是连接运算符的扩展,可以处理缺失信息。
- 左外连接 ⟕
取出左侧关系中所有与右侧关系中任一元组都不匹配的元组,用空值null填充所有来自右侧关系的属性,构成新的元组,并将其加入到自然连接的结果中。
sql举例
-- 左联结
SELECT customers.cust_id, orders.order_num
FROM customers
LEFT OUTER JOIN orders
ON customers.cust_id = orders.cust_id;- 右外连接 ⟖
取出右侧关系中所有与左侧关系中任一元组都不匹配的元组,用空值null填充所有来自左侧关系的属性,构成新的元组,并将其加入到自然连接的结果中。
sql举例
-- 右联结
select customers.cust_id,orders.order_num
from customers
right outer join orders
on customers.cust_id = orders.cust_id;- 全外连接 ⟗
同时完成左外连接和右外连接的操作。
不考
6️⃣ 聚集函数 function
聚集运算是关系代数运算中一个非常重要的扩展。
聚集函数输入一个值的集合,返回单一值作为结果。
常用的函数如下:
MySQL函数大全,MySQL常用函数合集 | 菜鸟成长记 (newbieup.com)
⚡ 相关真题
2014年36-39题

(36) A.4 B.5 C.6 D.8
(37)A.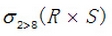
B.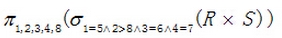
C. 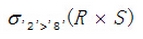
D.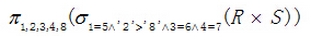
(38) A.R.A, R.B, R.C, R.D, S.E
B.R.A,R.C,R.D,S.C,S.D,S.E
C.A,B,C,D,A,C,D,E
D.R.A,R.B,R.C,R.D, S.A,S.C, S.D,S.E
(39) A.R.A=S OR R.B=S.E OR R.C=S.C OR R.D=S.D
B.R.A=S.A OR R.B>S.E OR R.C=S.C OR R.D=S.D
C.R.A=S.A AND R.B=S.E AND R.C=S.C AND R.D=S.D
D.R.A=S.A AND R.B>S.E AND R.C=S.C AND R.D=S.D
解析:B B A D
因为自然连接是一种特殊的等值连接,它要求两个关系中进行比较的分量必须是相同的属性组,并且在结果集中将重复属性列去掉。
2015年37/38题
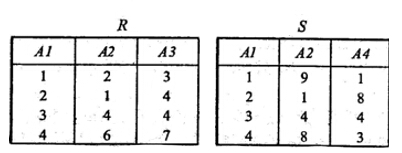
关系R、S如下表所示,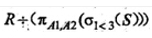 的结果为(37)
的结果为(37)
A. { 4 }
B. {3,4}
C. {3,4,7}
D. {(1,2), (2,1), (3,4), (4,7)}
,R、S的左外连接、右外连接和完全外连接的元组个数分别为(38).
A. 2,2,4
B. 2,2,6
C. 4,4,4
D. 4,4,6
【答案】A D
关系代数的除法运算是同时从关系的水平方向和垂直方向进行运算的。
若给定关系R(X,Y)和S(Y,Z),X、Y和Z为属性组,R÷S满足元组在X上的分量值x的象集Yx包含S在Y上投影的集合。记作:
R÷S={tr|tr∈R⋀ts[Y]⊆YX}
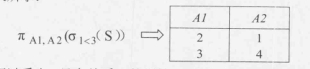
从上述分析可以看出,只有关系R的属性A3的值为4时,其象集包含了关系S在属性组X即(A1,A2)上的投影,所以R÷S={4}。
两个关系R和S进行自然连接时,选择两个关系R和S公共属性上相等的元组,去掉重复的属性列构成新关系。
左外联接是指与R与S进行自然连接时,只把R中舍弃的元组放到新关系中。
右外联接是指R与S进行自然连接时,只把S中舍弃的元组放到新关系中。
完全外联接是指R与S进行自然连接时,把R和S中舍弃的元组都放到新关系中。
R与S的左外联接、右外联接和完全外联接的结果如下表所示:
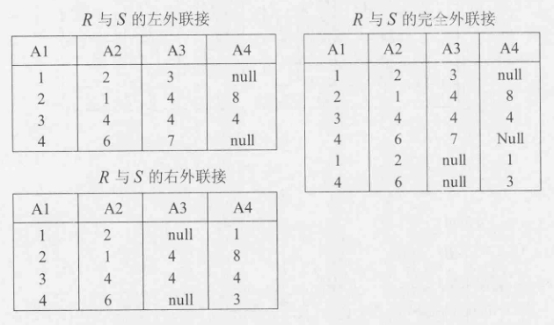
从运算的结果可以看出R与S的左外联接、右外联接和完全外联接的元组个数分别为4,4,6。
::: danger
注意全外连接的个数
:::